- 长臂猿-企业应用及系统软件平台
机器之心专栏 机器之心编辑部
蚂蚁 AI Infra 团队在深度学习最核心之一的优化器方向持续投入与创新，实现了 AI 训练节约资源、加速收敛、提升泛化等目标。我们将推出“优化器三部曲”系列，这是本系列的第一篇。
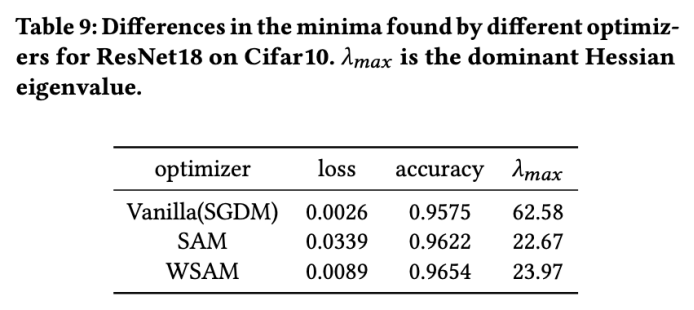
深度神经网络（DNNs）的泛化能力与极值点的平坦程度密切相关，因此出现了 Sharpness-Aware Minimization (SAM) 算法来寻找更平坦的极值点以提高泛化能力。本文重新审视 SAM 的损失函数，提出了一种更通用、有效的方法 WSAM，通过将平坦程度作为正则化项来改善训练极值点的平坦度。通过在各种公开数据集上的实验表明，与原始优化器、SAM 及其变体相比，WSAM 在绝大多数情形都实现了更好的泛化性能。WSAM 在蚂蚁内部数字支付、数字金融等多个场景也被普遍采用并取得了显著效果。该文被 KDD '23 接收为 Oral Paper。
论文地址：https://arxiv.org/pdf/2305.15817.pdf
代码地址：https://github.com/intelligent-machine-learning/dlrover/tree/master/atorch/atorch/optimizers
随着深度学习技术的发展，高度过参数化的 DNNs 在 CV 和 NLP 等各种机器学习场景下取得了巨大的成功。虽然过度参数化的模型容易过拟合训练数据，但它们通常具有良好的泛化能力。泛化的奥秘受到越来越多的关注，已成为深度学习领域的热门研究课题。
最近的研究表明，泛化能力与极值点的平坦程度密切相关，即损失函数“地貌”中平坦的极值点可以实现更小的泛化误差。Sharpness-Aware Minimization (SAM) [1] 是一种用于寻找更平坦极值点的技术，是当前最有前途的技术方向之一。它广泛应用于各个领域，如 CV、NLP 和 bi-level learning，并在这些领域明显优于原先最先进的方法。
为了探索更平坦的最小值，SAM 定义损失函数 L 在 w 处的平坦程度如下：
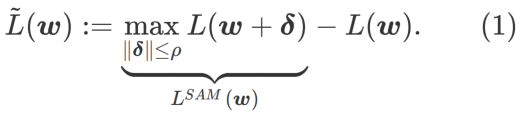
GSAM [2] 证明了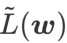 
是局部极值点 Hessian 矩阵最大特征值的近似，表明 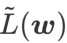确实是平坦（陡峭）程度的有效度量。然而 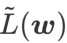只能用于寻找更平坦的区域而不是最小值点，这可能导致损失函数收敛到损失值依然很大的点（虽然周围区域很平坦）。因此，SAM 采用
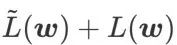，即 
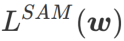作为损失函数。它可以视为在 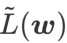和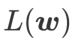 
之间寻找更平坦的表面和更小损失值的折衷方案，在这里两者被赋予了同等的权重。
本文重新思考了 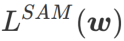的构建，将 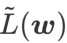视为正则化项。我们开发了一个更通用、有效的算法，称为 WSAM（Weighted Sharpness-Aware Minimization），其损失函数加入了一个加权平坦度项 
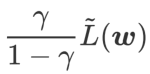作为正则项，其中超参数
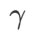控制了平坦度的权重。在方法介绍章节，我们演示了如何通过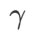来指导损失函数找到更平坦或更小的极值点。我们的关键贡献可以总结如下。
我们提出 WSAM，将平坦度视为正则化项，并在不同任务之间给予不同的权重。我们提出一个“权重解耦”技术来处理更新公式中的正则化项，旨在精确反映当前步骤的平坦度。当基础优化器不是 SGD 时，如 SGDM 和 Adam，WSAM 在形式上与 SAM 有显著差异。消融实验表明，这种技术在大多数情况下可以提升效果。
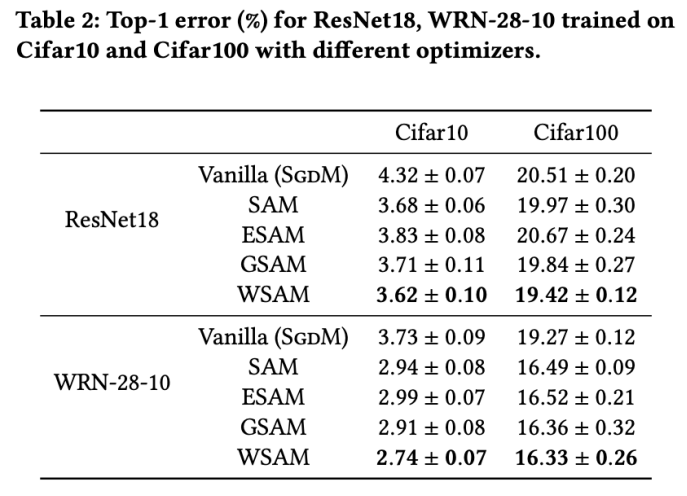
我们在公开数据集上验证了 WSAM 在常见任务中的有效性。实验结果表明，与 SAM 及其变体相比，WSAM 在绝大多数情形都有着更好的泛化性能。
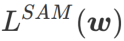的极小极大最优化问题的一种技术。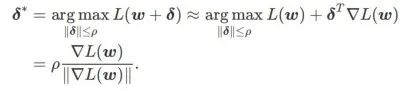
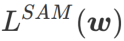的近似梯度来更新 w ，即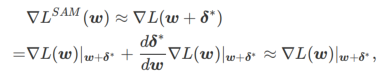
其中第二个近似是为了加速计算。其他基于梯度的优化器（称为基础优化器）可以纳入 SAM 的通用框架中，具体见Algorithm 1。通过改变 Algorithm 1 中的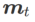 
和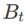
，我们可以获得不同的基础优化器，例如 SGD、SGDM 和 Adam，参见 Tab. 1。请注意，当基础优化器为 SGD 时，Algorithm 1 回退到 SAM 论文 [1] 中的原始 SAM。
在此，我们给出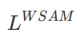
的正式定义，它由一个常规损失和一个平坦度项组成。由公式（1），我们有
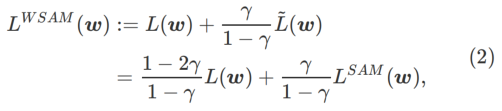
其中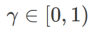 
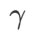。当=0 时，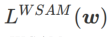
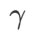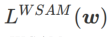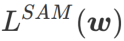退化为常规损失；当 =1/2 时， 等价于 ；当 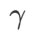>1/2 时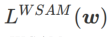， 更注重平坦度，因此与 SAM 相比更容易找到具有较小曲率而非较小损失值的点；反之亦然。
包含不同基础优化器的 WSAM 的通用框架可以通过选择不同的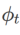 
和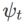 
来实现，见 Algorithm 2。例如，当 
和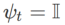 
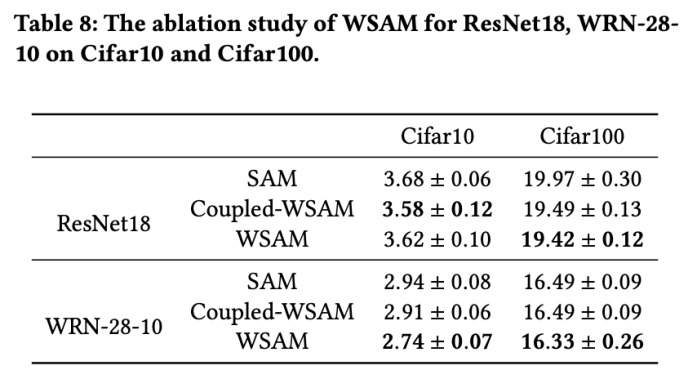
时，我们得到基础优化器为 SGD 的 WSAM，见 Algorithm 3。在此，我们采用了一种“权重解耦”技术，即 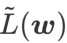平坦度项不是与基础优化器集成用于计算梯度和更新权重，而是独立计算（Algorithm 2 第 7 行的最后一项）。这样，正则化的效果只反映了当前步骤的平坦度，而没有额外的信息。为了进行比较，Algorithm 4 给出了没有“权重解耦”（称为 Coupled-WSAM）的 WSAM。例如，如果基础优化器是 SGDM，则 Coupled-WSAM 的正则化项是平坦度的指数移动平均值。如实验章节所示，“权重解耦”可以在大多数情况下改善泛化表现。
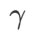取值下的 WSAM 更新过程。当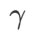<1/2 时，
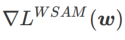介于 
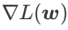和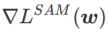 
之间，并随着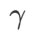增大逐渐偏离 。
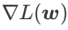为了更好地说明 WSAM 中 γ 的效果和优势，我们设置了一个二维简单示例。如 Fig. 2 所示，损失函数在左下角有一个相对不平坦的极值点（位置：(-16.8, 12.8)，损失值：0.28），在右上角有一个平坦的极值点（位置：(19.8, 29.9)，损失值：0.36）。损失函数定义为: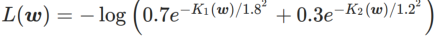 
，这里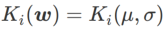 
是单变量高斯模型与两个正态分布之间的 KL 散度，即 
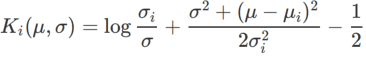，其中 
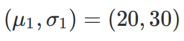和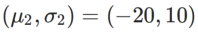 
。
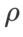=2 。从初始点 (-6, 10) 开始，使用学习率为 5 在 150 步内优化损失函数。SAM 收敛到损失值更低但更不平坦的极值点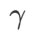，=0.6的 WSAM 也类似。然而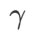，=0.95 使得损失函数收敛到平坦的极值点，说明更强的平坦度正则化发挥了作用。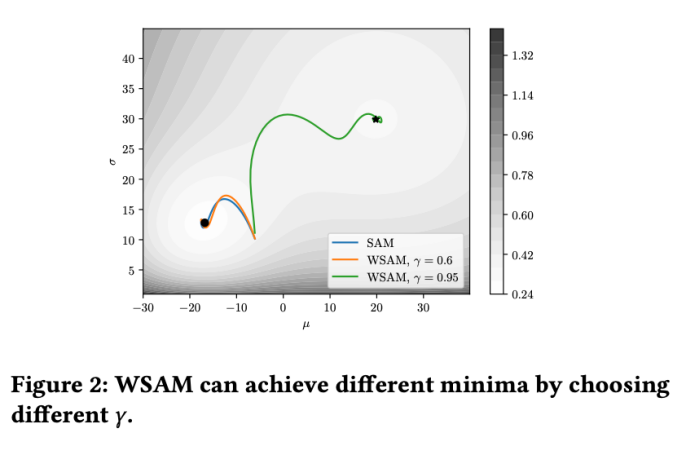
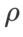(邻域大小)，我们接下来在 SAM 优化器上搜索最佳的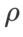并将相同的值用于其他 SAM 类优化器。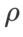的搜索范围为 {0.01, 0.02, 0.05, 0.1, 0.2, 0.5}。最后，我们对其他 SAM 类优化器各自独有的超参进行搜索，搜索范围来自各自原始文章的推荐范围。对于 GSAM [2]，我们在 {0.01, 0.02, 0.03, 0.1, 0.2, 0.3} 范围内搜索。对于 ESAM [3]，我们在 {0.4, 0.5, 0.6} 范围内搜索 
，在 {0.4, 0.5, 0.6} 范围内搜索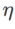 
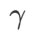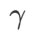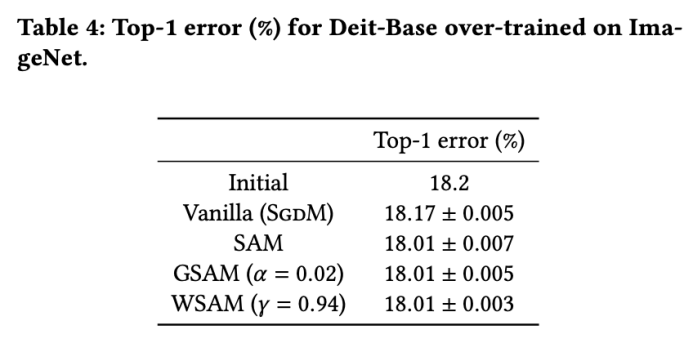
，在 {0.4, 0.5, 0.6} 范围内搜索。对于 WSAM，我们在 {0.5, 0.6, 0.7, 0.8, 0.82, 0.84, 0.86, 0.88, 0.9, 0.92, 0.94, 0.96} 范围内搜索。我们使用不同的随机种子重复实验 5 次，计算了平均误差和标准差。我们在单卡 NVIDIA A100 GPU 上进行实验。每个模型的优化器超参总结在 Tab. 3 中。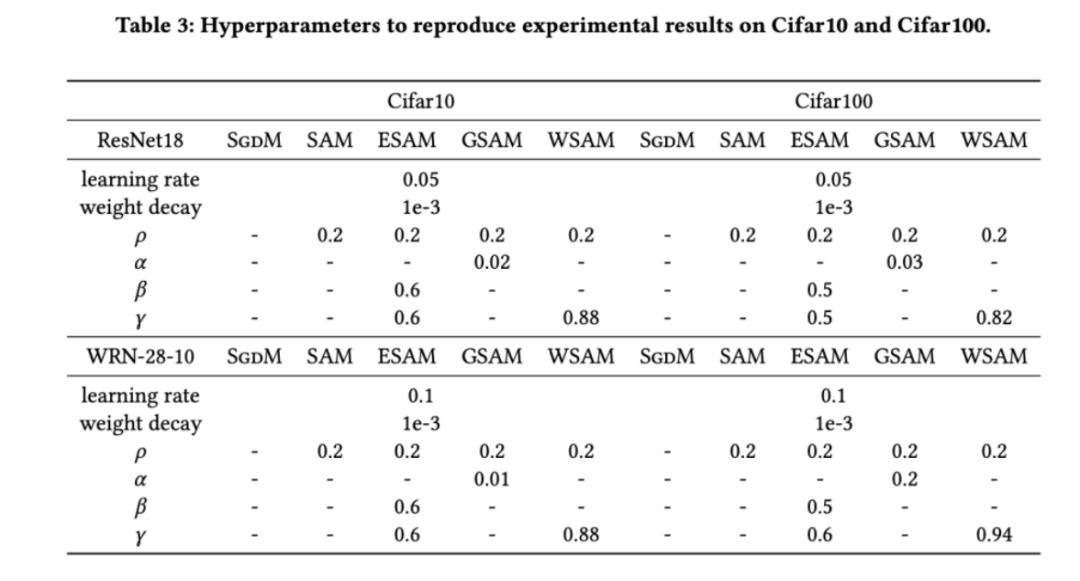
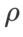。最佳的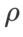=5.5 被直接用于其他 SAM 类优化器。之后，我们在{0.01, 0.02, 0.03, 0.1, 0.2, 0.3}中搜索 GSAM 的最佳 ，并在 0.80 到 0.98 之间以 0.02 的步长搜索WSAM 的最佳。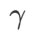
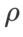值。然后，我们单独搜索其他优化器特定的超参数，以找到最优泛化性能。我们在 Tab. 5 中列出了复现我们结果所需的超参数。我们在 Tab. 6 中给出了鲁棒性测试的结果，WSAM 通常比 SAM、ESAM 和 GSAM 都具有更好的鲁棒性。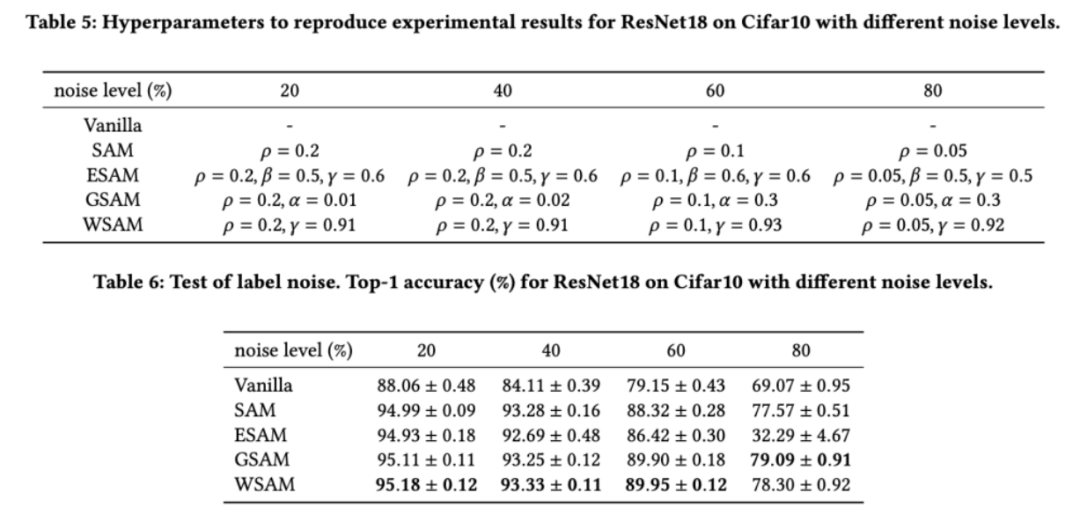
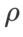和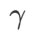之外的参数，我们复用了图像分类中的配置。根据先前的研究 [4, 5]，ASAM 和 Fisher SAM 的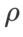通常较大。我们在 {0.1, 0.5, 1.0,…, 6.0} 中搜索最佳的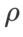，ASAM 和 Fisher SAM 最佳的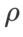均为 5.0。之后，我们在 0.80 到 0.94 之间以 0.02 的步长搜索 WSAM 的最佳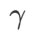，两种方法最佳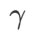均为 0.88。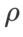基准 WSAM 即可。
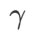，用于缩放平坦（陡峭）度项的大小。在这里，我们测试 WSAM 的泛化性能对该超参的敏感性。我们在 Cifar10 和 Cifar100 上使用 WSAM 对 ResNet18 和 WRN-28-10 模型进行了训练，使用了广泛的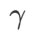取值。如 Fig. 3 所示，结果表明 WSAM 对超参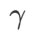的选择不敏感。我们还发现，WSAM 的最优泛化性能几乎总是在 0.8 到 0.95 之间。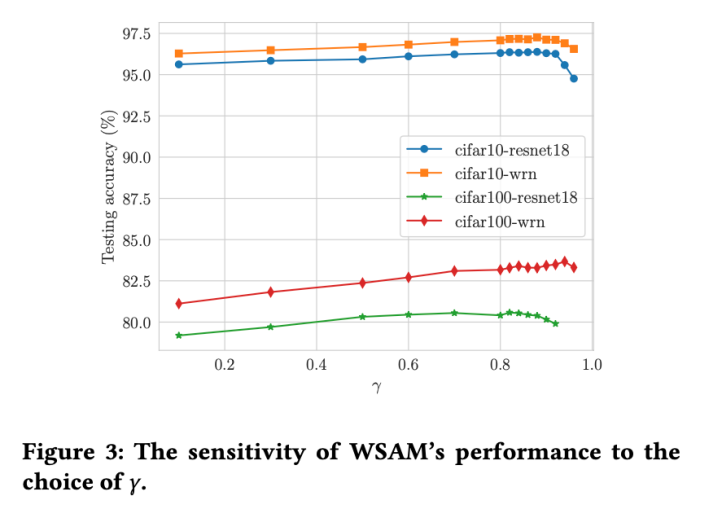
13分钟版本
© THE END
转载请联系本公众号获得授权
投稿或寻求报道：content@jiqizhixin.com