- 长臂猿-企业应用及系统软件平台


机器之心专栏
本⽂介绍⼀项近期的研究⼯作,试图建⽴能量约束扩散微分⽅程与神经⽹络架构的联系,从而原创性的提出了物理启发下的 Transformer,称作 DIFFormer。作为⼀种通⽤的可以灵活⾼效的学习样本间隐含依赖关系的编码器架构,DIFFormer 在各类任务上都展现了强大潜⼒。这项工作已被 ICLR 2023 接收,并在⾸轮评审就收到了四位审稿⼈给出的 10/8/8/6 评分(最终均分排名位于前 0.5%)。


 个节点,每个节点有初始的温度,两两节点之间都存在信号流动,随着时间的推移节点的温度会不断更新。上述物理过程事实上可以类⽐的看作深度神经网络计算样本表征(embedding)的前向过程。
个节点,每个节点有初始的温度,两两节点之间都存在信号流动,随着时间的推移节点的温度会不断更新。上述物理过程事实上可以类⽐的看作深度神经网络计算样本表征(embedding)的前向过程。
 个样本的数据集,用
个样本的数据集,用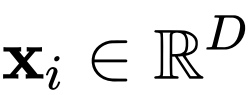 表示样本 i 的输入特征,
表示样本 i 的输入特征, 表示样本 i 的表征向量。⼀个 L 层的神经网络模型会把每个输⼊样本映射到⼀系列隐空间中的表征向量:
表示样本 i 的表征向量。⼀个 L 层的神经网络模型会把每个输⼊样本映射到⼀系列隐空间中的表征向量: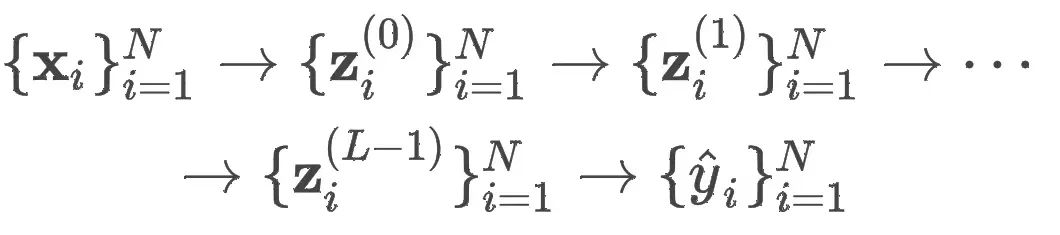

 ,
, 和
和 分别表示梯度(gradient)算⼦、散度 (divergence) 算⼦和扩散率(diffusivity)。对于由 N 个节点组成的离散化空间,以上三个概念的具体定义可以如下表示:
分别表示梯度(gradient)算⼦、散度 (divergence) 算⼦和扩散率(diffusivity)。对于由 N 个节点组成的离散化空间,以上三个概念的具体定义可以如下表示: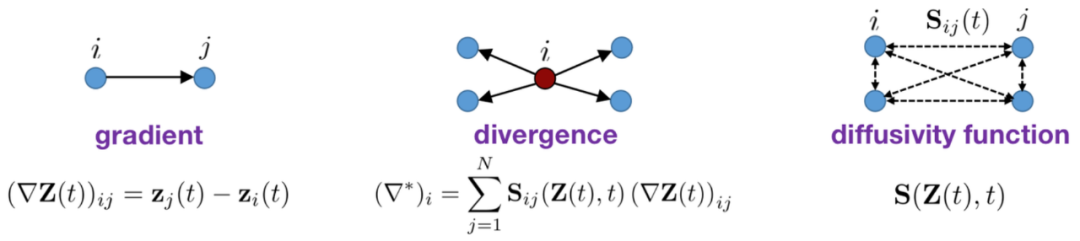

 定义了在当前时刻任意两两节点
定义了在当前时刻任意两两节点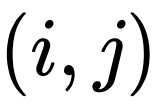 之间的影响,即信号从节点
之间的影响,即信号从节点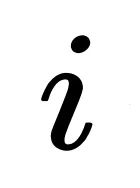 流向
流向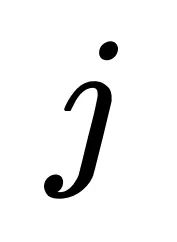 的速率的⼀种度量。
的速率的⼀种度量。 对连续时间进⾏离散化(再经过⽅程左右重新整理):
对连续时间进⾏离散化(再经过⽅程左右重新整理):
 是经过沿⾏归⼀化的),于是上式就可以视为⼀个对其他样本表征的信息聚合(第⼆项)再加上⼀个对上⼀层⾃身表征的 residual 连接(第⼀项)。这⾥的扩散率
是经过沿⾏归⼀化的),于是上式就可以视为⼀个对其他样本表征的信息聚合(第⼆项)再加上⼀个对上⼀层⾃身表征的 residual 连接(第⼀项)。这⾥的扩散率 是⼀个
是⼀个 的矩阵,我们可以对其进⾏不同的假设,就可以得到不同模型的层间更新公式:
的矩阵,我们可以对其进⾏不同的假设,就可以得到不同模型的层间更新公式: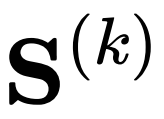 是⼀个
是⼀个 的单位矩阵:(1)式中每个样本的表征计算只取决于⾃⼰(与其他样本独⽴),此时给出的是 Multi-Layer Perceptron (MLP) 的更新公式,即每个样本被单独输⼊进 encoder 计算表征;
的单位矩阵:(1)式中每个样本的表征计算只取决于⾃⼰(与其他样本独⽴),此时给出的是 Multi-Layer Perceptron (MLP) 的更新公式,即每个样本被单独输⼊进 encoder 计算表征;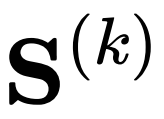 在固定位置存在⾮零值(如输⼊图中存在连边的位置):(1)式中每个样本的表征更新会依赖于图中相邻的其他节点,此时给出的是 Graph Neural Networks (GNN) 的更新公式,其中
在固定位置存在⾮零值(如输⼊图中存在连边的位置):(1)式中每个样本的表征更新会依赖于图中相邻的其他节点,此时给出的是 Graph Neural Networks (GNN) 的更新公式,其中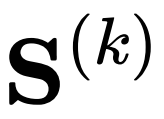 是传播矩阵(propagation matrix),例如图卷积⽹络(GCN)模型采⽤归⼀化后的邻接矩阵
是传播矩阵(propagation matrix),例如图卷积⽹络(GCN)模型采⽤归⼀化后的邻接矩阵 ;
;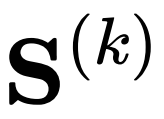 在所有位置都允许有⾮零值,且每层的
在所有位置都允许有⾮零值,且每层的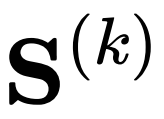 都可以发⽣变化:(1)式中每个样本的表征更新会依赖于其他所有节点,且每次更新两两节点间的影响也会适应性的变化,此时 (1) 式给出的是 Transformer 结构的更新公式,
都可以发⽣变化:(1)式中每个样本的表征更新会依赖于其他所有节点,且每次更新两两节点间的影响也会适应性的变化,此时 (1) 式给出的是 Transformer 结构的更新公式,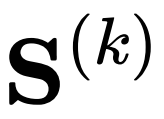 表示第
表示第 层的 attention 矩阵。
层的 attention 矩阵。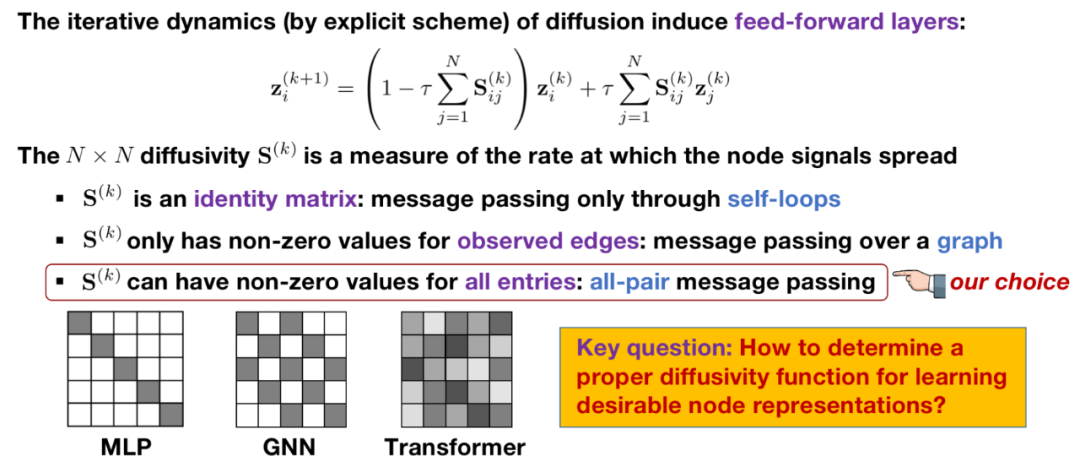
 ,其对应的能量定义为:
,其对应的能量定义为:
 是⼀个单调递增的凹函数(当
是⼀个单调递增的凹函数(当 与
与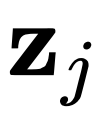 差别较⼤时,
差别较⼤时, 会返回⼀个适中的能量值,即减⼩对差异较⼤的节点对
会返回⼀个适中的能量值,即减⼩对差异较⼤的节点对 的“惩罚”,这有助于提升样本表征的 diversity)。理想情况下,当系统的整体能量达到最⼩化,我们可以认为系统中的每⼀个个体都与整体取得了平衡,样本的表征同时吸收了局部和全局的信息。
的“惩罚”,这有助于提升样本表征的 diversity)。理想情况下,当系统的整体能量达到最⼩化,我们可以认为系统中的每⼀个个体都与整体取得了平衡,样本的表征同时吸收了局部和全局的信息。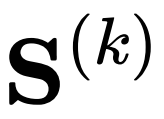 被定义为⼀个待优化的隐变量,我们希望它给出的每⼀步的节点表征都能够使得系统整体的能量下降。带能量约束的扩散过程可以被形式化的描述为:
被定义为⼀个待优化的隐变量,我们希望它给出的每⼀步的节点表征都能够使得系统整体的能量下降。带能量约束的扩散过程可以被形式化的描述为:
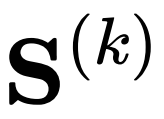 ⾮常复杂(因为他耦合了每⼀步能量下降的约束),不过本⽂通过理论分析建⽴了扩散⽅程数值迭代与能量优化梯度更新的等价性,从⽽得到了每⼀步扩散率的最优闭式解。
⾮常复杂(因为他耦合了每⼀步能量下降的约束),不过本⽂通过理论分析建⽴了扩散⽅程数值迭代与能量优化梯度更新的等价性,从⽽得到了每⼀步扩散率的最优闭式解。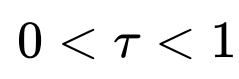 和相应的扩散率估计
和相应的扩散率估计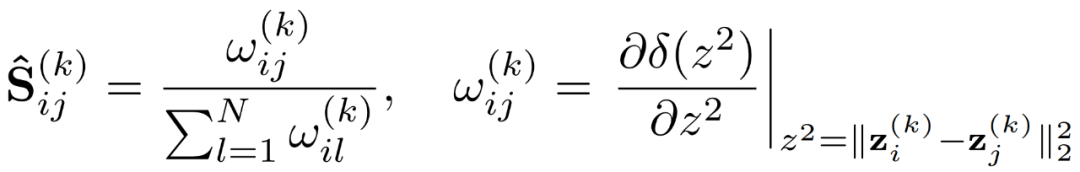
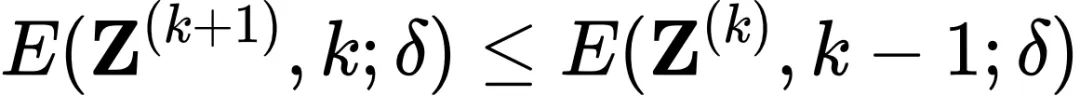 。
。
 表示衡量
表示衡量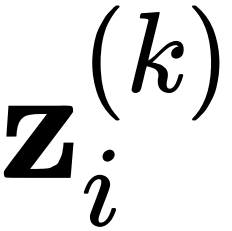 和
和 相似性的函数,在具体设计时具有很⼤的灵活性。下⾯我们提出两种具体设计,分别称相应的模型结构为 DIFFormer-s 和 DIFFormer-a。
相似性的函数,在具体设计时具有很⼤的灵活性。下⾯我们提出两种具体设计,分别称相应的模型结构为 DIFFormer-s 和 DIFFormer-a。

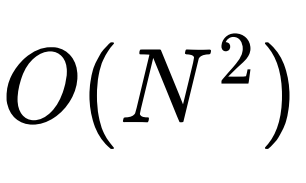 平⽅复杂度。庆幸的是,这⾥ DIFFormer-s 的 attention 定义可以保证每⼀层更新
平⽅复杂度。庆幸的是,这⾥ DIFFormer-s 的 attention 定义可以保证每⼀层更新 个样本表征的计算复杂度在
个样本表征的计算复杂度在 之内,这⾮常有利于提升模型的时空效率(特别是空间效率,当需要扩展到包含⼤量样本的数据集时)。
之内,这⾮常有利于提升模型的时空效率(特别是空间效率,当需要扩展到包含⼤量样本的数据集时)。 复杂度呢?
复杂度呢? 代⼊更新单个样本的聚合公式,然后通过矩阵乘法结合律交换矩阵运算的顺序(这⾥假设
代⼊更新单个样本的聚合公式,然后通过矩阵乘法结合律交换矩阵运算的顺序(这⾥假设 ):
):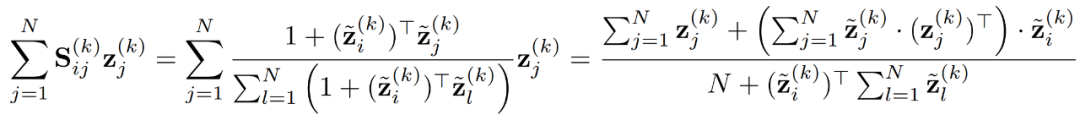
 复杂度,⽽⼜因为这是对单个样本的更新公式,因此更新
复杂度,⽽⼜因为这是对单个样本的更新公式,因此更新 个不同的样本需要的复杂度是。但在右边的式⼦中,分⼦和分⺟的两个求和项对于所有样本是共享的,也就是说在实际计算中只需要
个不同的样本需要的复杂度是。但在右边的式⼦中,分⼦和分⺟的两个求和项对于所有样本是共享的,也就是说在实际计算中只需要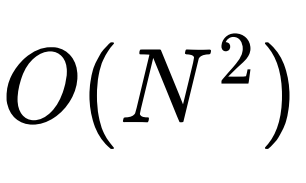 算⼀次,⽽后对每个样本的更新只需要
算⼀次,⽽后对每个样本的更新只需要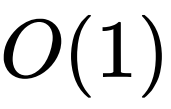 ,因此更新
,因此更新 个样本的总复杂度是
个样本的总复杂度是 。不过对于 DIFFormer-a 的 attention 设计,则⽆法保证
。不过对于 DIFFormer-a 的 attention 设计,则⽆法保证 的计算复杂度,因为⾮线性的引⼊导致了⽆法交换矩阵运输的次序。下图总结了两个模型在具体实现(采⽤矩阵乘法更新⼀层所有样本的表征)中的运算过程。
的计算复杂度,因为⾮线性的引⼊导致了⽆法交换矩阵运输的次序。下图总结了两个模型在具体实现(采⽤矩阵乘法更新⼀层所有样本的表征)中的运算过程。
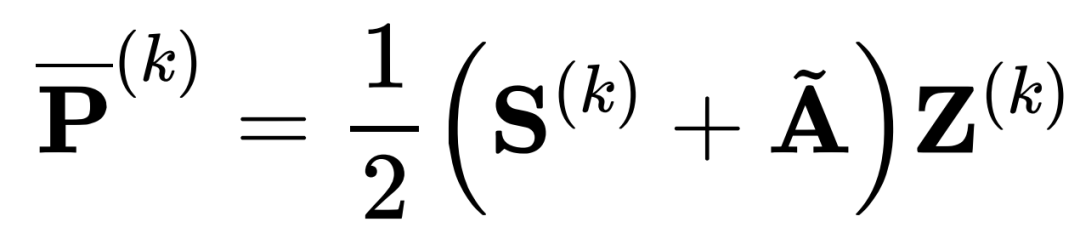
 ,
, 表示输⼊图,
表示输⼊图,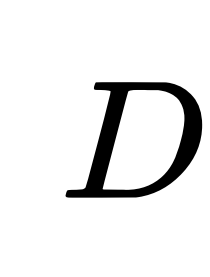 表示其对应的(对⻆)度矩阵。
表示其对应的(对⻆)度矩阵。






 复杂度来更新
复杂度来更新 个节点的表征,同时兼容 mini-batch training,可以有效扩展到⼤规模数据集。
个节点的表征,同时兼容 mini-batch training,可以有效扩展到⼤规模数据集。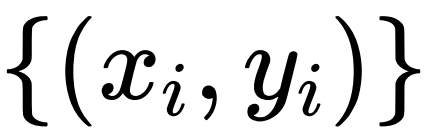 ,样本间的依赖关系未知。此时 DIFFormer 可⽤于学习样本间的隐式依赖关系,利⽤全局信息来计算每个样本的表征。这是⼀个较少被研究的领域,传统⽅法的主要 bottleneck 是在⼩数据集上容易过拟合(由于考虑了样本依赖模型过于复杂),⼤数据集上⼜⽆法有效扩展(学习任意两两样本的关系带来了平⽅复杂度)。DIFFormer 的优势在于简单的模型结构有效避免了过拟合问题,⽽且保证了相对于样本数量的
,样本间的依赖关系未知。此时 DIFFormer 可⽤于学习样本间的隐式依赖关系,利⽤全局信息来计算每个样本的表征。这是⼀个较少被研究的领域,传统⽅法的主要 bottleneck 是在⼩数据集上容易过拟合(由于考虑了样本依赖模型过于复杂),⼤数据集上⼜⽆法有效扩展(学习任意两两样本的关系带来了平⽅复杂度)。DIFFormer 的优势在于简单的模型结构有效避免了过拟合问题,⽽且保证了相对于样本数量的 复杂度可以有效扩展到⼤规模数据集。
复杂度可以有效扩展到⼤规模数据集。 作为⼀般的即插即⽤式 encoder,解决各式各样的下游任务(如⽣成 / 预测 / 决策问题)。此时 DIFFormer 可以直接⽤于⼤框架下的某个部件,得到输⼊数据的隐空间表征,⽤于下游任务。相⽐于其他 encoder (如 MLP/GNN/Transformer),DIFFormer 的优势在于可以⾼效的计算全局 attention,同时具有⼀定的理论基础(能量下降扩散过程的观点)。

© THE END
转载请联系本公众号获得授权
投稿或寻求报道:content@jiqizhixin.com
本文来自机器之心